论文粗读(2)：多目标推荐模型

CTCVR拆解/多任务融合方案：ESMM

背景

ESMM主要想要解决的是样本稀疏预测问题。比如在视频、电商推荐领域，模型最终目标是推出用户真正感兴趣的物品，即“点击并购买”、“点击并完播”的物品。在推荐场景，点击率称为CTR，而转化率称为CVR，因此，我们拟合的“点击转化率”就是CTCVR。但是，由于推出的海量物品中，用户本身的点击行为就是稀疏的，更不要提还有众多标题党、劣质商品混杂其中，本身“点击并转化”的物品数量就非常之少。因此，在正负样本比例极度失衡的情况下，直接拟合CTCVR一般得到的模型效果并不是很好。

但是，在点击和转化中，二者是两个相对独立的过程。比如一个视频，用户产生点击反映的是用户看简介，而完播则是反映的用户看视频本体。因此用户对一个物品x的CTCVR概率一般可以近似分解为如下形式：

$$pCTCVR(x)=pCTR(x)×pCVR(x)$$

这个简单的概率公式也是ESMM的理论基础

ESMM模型结构

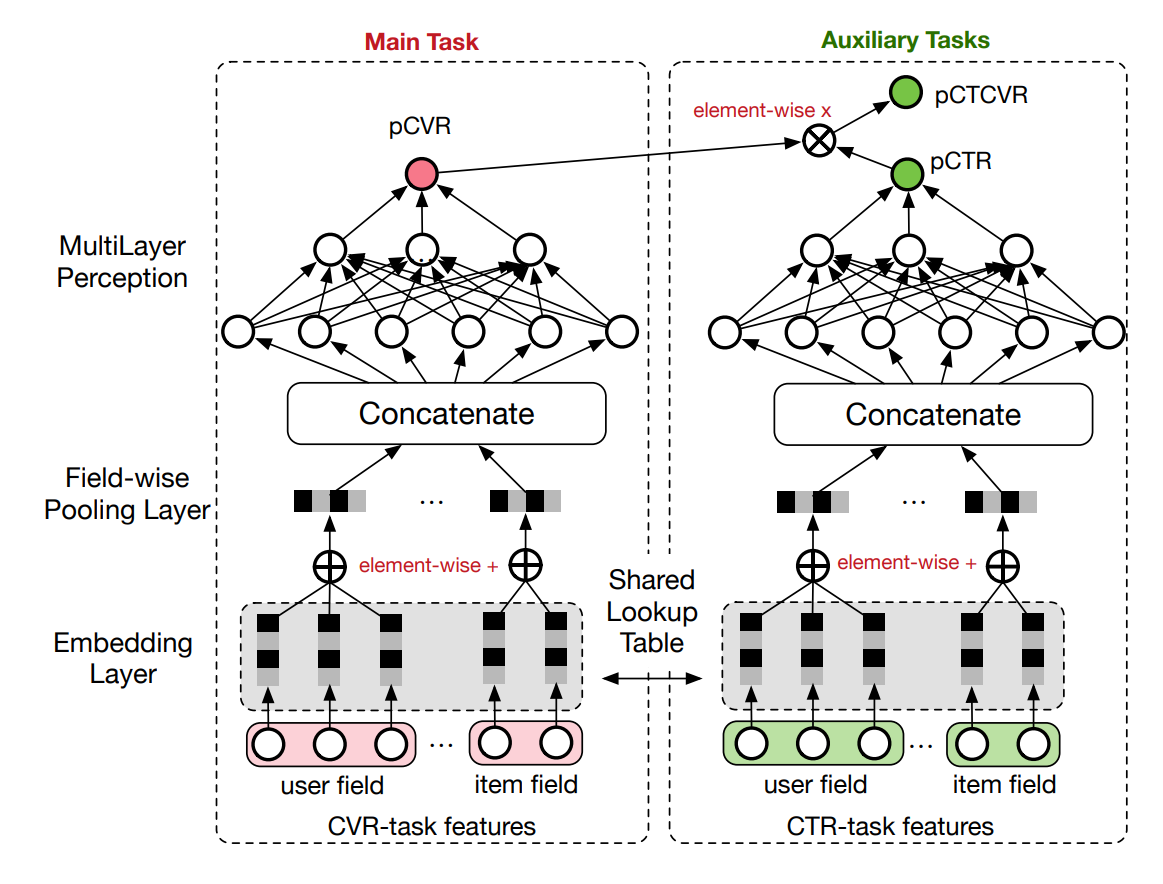
ESMM model

ESMM模型结构如上图所示，核心思想即上面将到的概率公式，由于点击和转化相对独立，因此它就将CTCVR任务拆开成了两个任务，分别构建了CTR和CVR两个MLP子塔来进行优化，并把结果相乘，获得最终的CTCVR的预估分数。而说实话模型内部子塔细节没有什么可讲的，都是业界已经用烂的embedding+MLP单目标模型。重点是目标拆分与融合、loss设计

Loss设计

从模型结构来看，虽然将CTR和CVR分为了两个任务，但ESMM还是没法解决CTCVR难以拟合的根因“正负样本比例极度失衡”的问题。因此，事实上ESMM解决此问题的着手点是在Loss设计上进行的，ESMM的Loss结构如下：

$$L(\theta_{CVR}, \theta_{CTR}) = \sum_{i=1}^N l(y_i,f(x_i;\theta_{CTR})) + \sum_{i=1}^N l(y_i \And z_i,f(x_i;\theta_{CTR}) \times f(x_i;\theta_{CVR}))$$

其中$\sum_{i=1}^N l(y_i,f(x_i;\theta_{CTR}))$表示的是CTR子塔的输出与“真实点击与否”正负样本的交叉熵，而$\sum_{i=1}^N l(y_i \And z_i,f(x_i;\theta_{CTR}) \times f(x_i;\theta_{CVR}))$则是CTR子塔输出乘以CVR子塔输出结果并和“真实点击并交互与否” 的正负样本的交叉熵。值得注意的是这里的交叉熵是并非一般的使用logits计算而是使用prediction label计算。因为prediction即是预测概率，而logits并不表示预测概率， logits相乘并无意义

这样设计的好处是首先我们通过拟合CTR loss，首先我们可以获得对于某个物品用户点击与否的意愿，然后再将输出结果作为点击概率乘到CVR子塔输出上，那么$f(x_i;\theta_{CTR}) \times f(x_i;\theta_{CVR})$就应该是用户点击并交互的概率，通过和真实label求loss即可拟合CTCVR

可能有人会问为啥Loss第二项不是$\sum_{i=1}^N l(z_i,f(x_i;\theta_{CVR}))$而是二者的相乘。这就是ESMM巧妙的一点，由于点击数据较少，CVR拟合的数据本身就很少，因此直接拟合其Loss的话效果并不会特别好，可能会漏掉海量数据中此用户可能感兴趣但还没曝光看过的物品。而拟合二者的相乘，pCTR的结果相当于给了所有曝光数据一个平滑操作，也给了那些优质内容且用户感兴趣但用户还没留意到的数据一些机会

还有人可能会问两个loss直接相加是否太过简单粗暴了点？我曾经也提出过这样的问题，后来观察模型训练loss时发现除非模型训崩，一般模型训练时每种loss本身都是以很快的指数来下降，那么即使最开始这两个子loss数量级并不均等，在几个epoch的迭代后二者很快就会下降至同一数量级，可能最开始模型只专注于某个子塔的优化，但随着训练的不断迭代，最终两个目标都会得到训练。当然训练效果是否完美则另当别论，因为一旦涉及到多目标模型，那么“负迁移”（或称“跷跷板”）问题就会如同鬼魅般随行

目标融合

前面提到，模型最终预测结果是pCTR乘以pCVR。然而，工业界实践时预测并不会直接使用相乘结果进行输出，而是会根据实际情况根据当前运营需要结合“想让用户更多使用软件浏览内容”、“推出更优质内容”来进行后处理加权。而在搜索广告领域，CTR就是用户点击物品， CVR就是用户点击物品产生的收益(普通物品就是0，广告物品就是其相应收益)，CTCVR即是广告收益，通过模型预测得到相应子塔结果后，后处理加权来控制“推出更优质内容”和“推出竞价排名更高”的物品（从这来看百度的CVR结果给的权值是相当的高hhh）

一般来说，业界现在Loss融合方式基本就是如下两种。其中$w_{CTR}$和$w_{CVR}$是人工定义并运营干预调节的参数

$$相乘形式：F(x) = f(x;CTR)^{w_{CTR}} \times f(x;CVR)^{w_{CVR}}$$

$$相加形式：F(x)= w_{CTR} \times f(x;CTR)+ w_{CVR} \times f(x;CVR)$$

相乘形式和相加形式唯一的差别就是f(x)过不过一个log，毕竟一般排序只是要看各个item的相对位置，而若你把相乘形式右式加一个log，就会发现只不过是底下相加形式的$w \times f(x)$变成了$w \times log(f(x))$，但一般相乘形式用的更多，主要原因还是相乘可以算一个总的AUC，具体做法是把各任务label相乘即是0-1分布的总label，然后可以通过总AUC来看出为了业务收益调节加权对CTCVR的损害程度，而相加形式则还需进行label相加后重新0-1离散化。此外相加形式调节过于线性，参数细微变动推荐结果就会产生大变化，调节起来更为麻烦

同样，如果模型本身优化目标就是一个多任务模型，那么也可以借鉴ESMM的方案，将其分为多个子塔，然后最终通过分析各个任务间的统计相关关系，构建相应地loss，并且在最终预测时将其融合起来

多任务模型的改进：MMOE和PLE

背景

ESMM模型说实话已经有些年头了，很多人可能都了解并用过这个模型，而用过的人肯定都有这样的体会：“虽然最终的CTCVR提升了，但CTR略有下降，就这样了吧”。而在当时的年代，凡是提起多目标，那么一个话题永远绕不过，那就是“负迁移”或者“跷跷板”问题。跷跷板问题是指也当进行多目标优化时，优化后每个目标的指标一般都不如单目标优化的指标。而如果调节网络使其中一个目标的指标变好时，另一个目标的指标通常会变差。这是因为“没有免费的午餐”定律，当模型分心进行多个loss的优化时，往往其并不会像单目标一样专注于一个loss，而是专注优化与对总loss贡献最大的子塔而忽视甚至放任其他任务子塔的上涨。举个例子，假设现在任务有两个子塔，总loss为二者loss相加，优化塔A可以降低其loss 10,但会提升塔B的loss 0.5。优化塔B可以降低其loss 5,但会提升塔A的loss 0.01。可看到虽然优化塔B对二者的损伤最小，但梯度优化最大化的方向却是只优化塔A。

对于跷跷板效应的解决，学术界和工业界也有很多的讨论。主要方法有两种，一是通过优化loss入手，即监测梯度，并把每个任务的梯度归一化到一个量级，这方面可参考苏神的博客系列多任务学习漫谈。二则是从任务隔离出发，即让模型有完全独立的部分处理各个任务，又有公共的部分让其学习共有的联系。这方面典型的模型有MMOE、PLE

MMOE模型结构

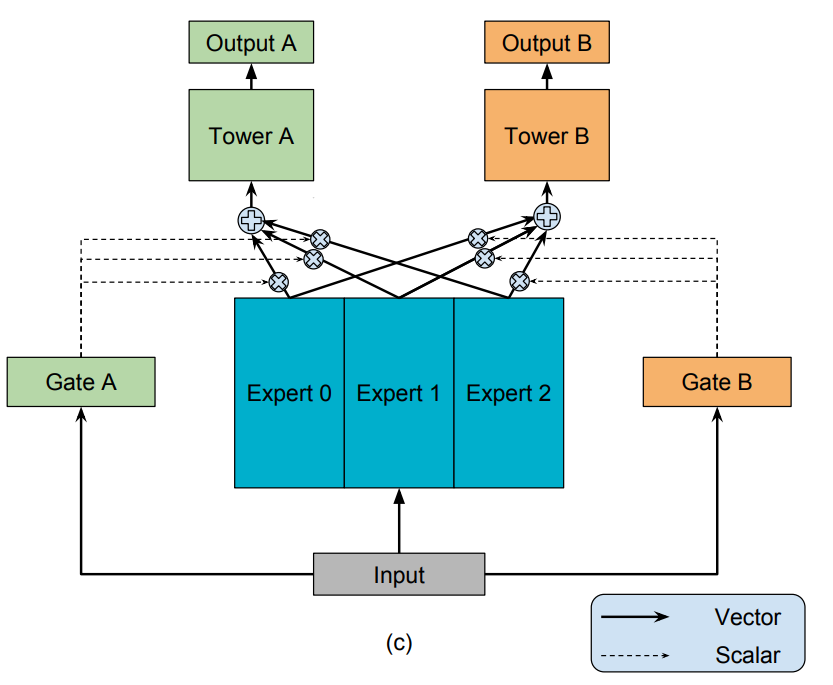
MMOE model

MMOE模型结构如上图所示，可以看到其相对于直接“底层网络+多个任务顶层网络”的区别主要是通过一个“专家+门控”的方式来模型的相对隔离。整个模型可以使用下数学表达式来表示：

$$y_k = h^k(f^k(x))$$

$$其中f^k(x) = \sum_{i=1}^N g^k(x)_if_i(x)$$

式中$y_k$表示第k个任务塔的输出，$h_k$表示第k个任务塔，$f^k(x)$表示第k个塔的输入，$g^k(x)_i$表示第i个门控对第k个塔的输出，$f_i(x)$则是第i个专家塔的输出。通俗的话来讲就是，模型的输入先经过i个专家网络，然后通过门控网络进行加权，再送到各个任务子网络中去

MMOE的“专家+门控”机制保证了使得在多个任务完全隔离的情况下，门控可以通过学习成为one-hot向量的方式，让网络事实成为多个分离的塔。而在各个任务基本一致的情况下，门控可以学习成为均匀向量来使得多个专家塔变为一个底层网络。一般来说，门控网络是通过“一层线性变换+softmax”的方式实现，而由于专家塔无论深浅，都可通过门控实现“完全分离”到“完全共享”，所以一般实现都是比较浅层的网络，有些实现甚至都是仅单层MLP（不过个人认为单层也太精简了。。。）

MMOE模型效果

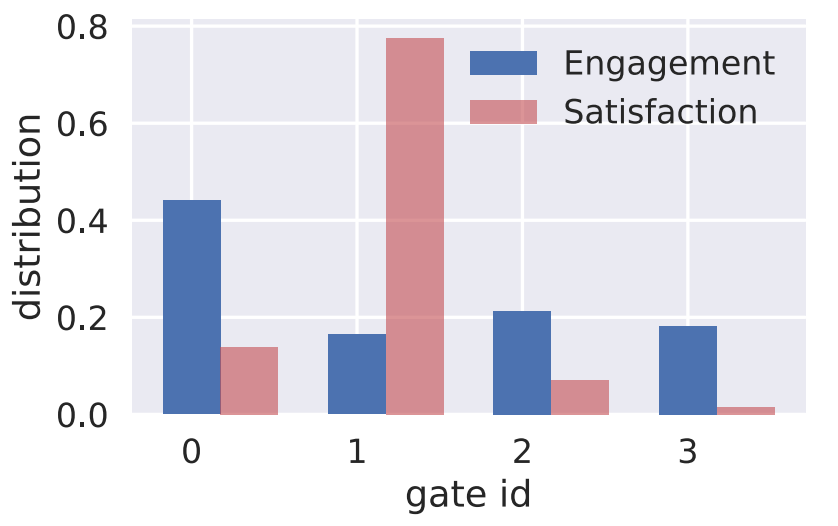
MMOE gate

上图显示了在订婚广告数据集上训练的“订婚-满意度”4专家双任务MMOE模型，训练后某样本中各个门控的输出值。可看出，各个专家门控对每个任务的输出都不相同，说明此结构是起作用的

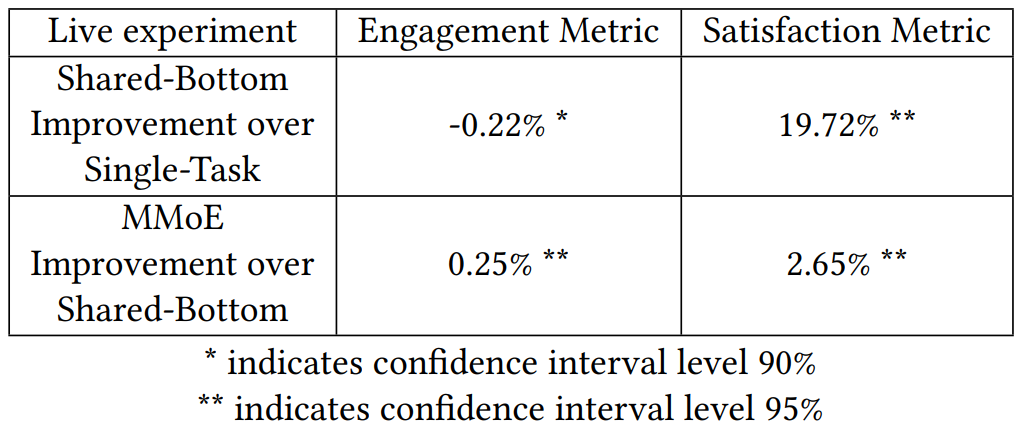
MMOE result

上图则显示了底层硬共享和MMOE模型相对于两个单任务模型的线上效果比较，可看到底层硬编码模型相对于单任务模型。其广告订婚率有所下降，但满意度有较大提升（毕竟满意度预测本身就比较难），有一定的跷跷板效应。而MMOE模型则实现了广告订婚率、满意度的双提升

PLE模型结构

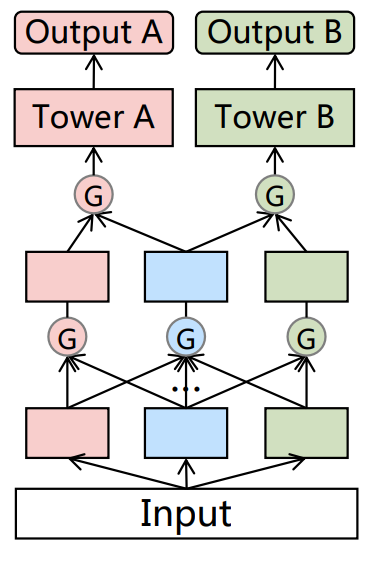
MMOE model

懂了MMOE模型后，之后的PLE模型、AESM^2模型等基本就都比较好懂了，因为它们都是MMOE模型的延伸。PLE模型结构如上图所示，其相对于MMOE模型主要拓展了两部分

将专家手动分为了共享专家（蓝色节点）和独有专家（红、绿色节点）。其中共享专家可以流向之后所有的层和塔，而独有专家则只可流向对应的任务专家层/塔和共享专家层。在节点融合时，仍然采用MMOE的门控加权方案
堆叠专家层而非只使用一层专家层，而每个专家层节点都只是一层MLP，其实也就是把原来的几个独立的MLP专家层变为每单层后都各个专家可以有交互的结构

总结PLE可以看出，这是一个工业设计感很强的模型，通过强行设定“共享专家”和“独有专家”强制性让一部分节点只为专有任务服务，一部分节点为所有任务服务，防止MMOE在任务较难区分时学习困难。再通过让每一层结果的所有独有专家可以通过门控也汇入共享专家，实现各个专家之间信息的共享，而非各专家各学各的，最后再一次加权。从逻辑上讲，这些设计基本相当于给原本的全交给数据自由学习变为人为结构设计给参数学习限定下方向，而这个方向基本也就是参数应该更新的方向，绝大多数情况也不会有什么损害

PLE模型效果

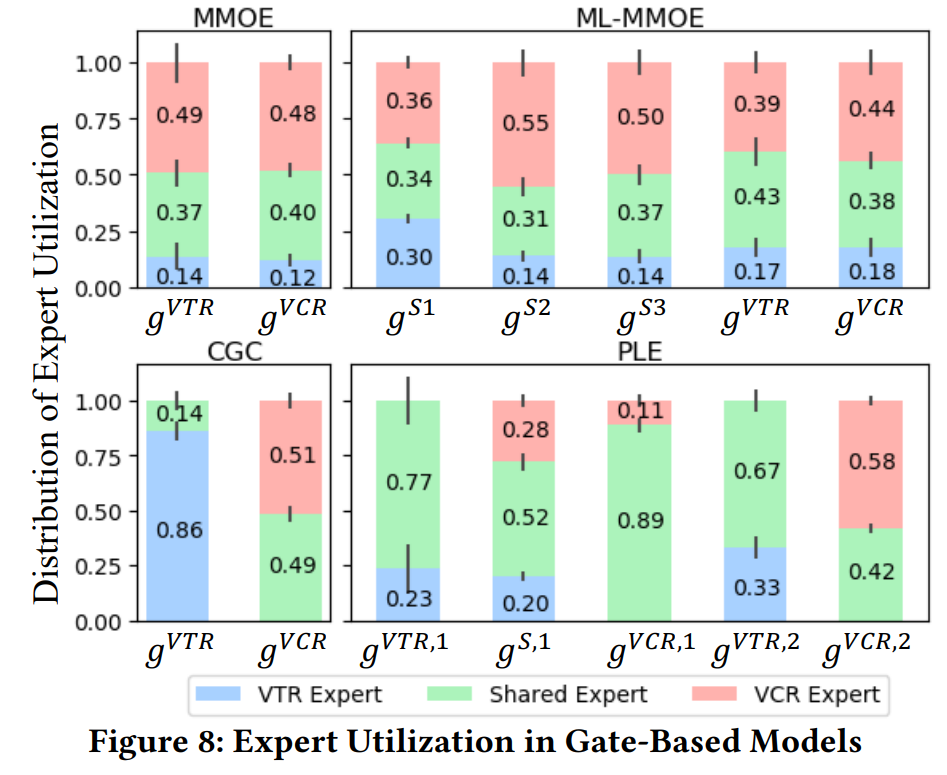
PLE gate

上图显示了在公共数据集上MMOE、CGC（单层PLE）、MT-MMOE（多层MMOE堆叠）和PLE的各个门控的输出值，从上可看出两点：一是这个数据集的VTR和VRC真的很难区分，可看到MMOE的两个门控输出权重基本一致。二是可看出PLE由于人为限定了独有专家，所以还可以做到每个门控输出不一致，不过如果仔细看$g^{S,1}$这个共享专家的输出结果，其和MMOE的结果基本类似，也就是说此场景共享专家其实效果也就和MMOE一样。而独有-共享融合时的专家输出的权重比例，也和MMOE中各任务的比例类似，比如$g^{VTR}$这个门控中PLE和MMOE的结果，$0.77/0.23$和$0.43/0.17$ 也相差不大。也就是说几个门控的权重变化基本就是由于“共享-独有”这种手动结构设计所带来的

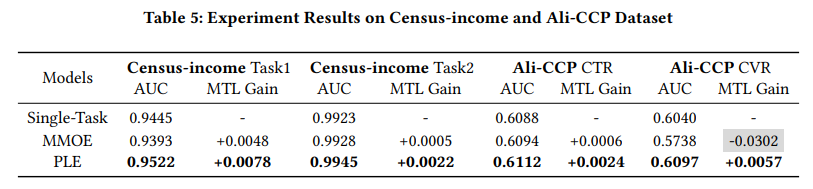
PLE result

模型离线结果，可看到在此数据集上PLE相对MMOE确实有提升，也就是说人为设定“共享-独有”方式确实是有效的，使用一般都会有好的提升

多场景学习模型：STAR

背景

相较于优化“点击”、“时长”、“用户满意”等多个不同指标的多任务模型，多场景模型则聚焦在不同场景下优化同一个目标，比如在搜索页、猜你想问页、随机推荐页来同时优化CTR目标。使用多场景模型的原因主要如下：

维护性问题：如果每个场景都维护一个模型，那么对于存储、计算资源、在线服务代码构建都需要进行相应维护。随着业务拓展，场景的不断增多，维护成本将会近似于线性增长，这一般是不可接受的。此外，不同场景下训练数据量级并不相同，有的场景曝光很少，通过有限的数据很难训练出一个效果较好的模型
共性问题知识迁移：对于用户来说，特定条件下对于物品的兴趣一般是相对稳定的。比如在进入电商后，用户主动进行寻找商品的前提下，主动搜索与看到首页曝光物品点击一般都是用户的兴趣点。因此通过一个模型学习可以在不同推荐模块下实现数据互补。此外，在推荐冷启动中，另一个场景已挖掘到的用户特征也会对新拓展的场景有所裨益
简单单目标模型负迁移问题：当然，这并不意味着在多场景下，构建一个简单的embedding+MLP单目标模型即可描述。因为在多场景下不同场景关注点还是有所区分，比如电商和搜索页，首页一般还承担“主动发现、提供给用户可能兴趣点”的任务，而搜索页则更要关注文本相关性。而不同场景下训练数据也使得单目标模型会更偏向优化某个数据量级大的模型而忽视数据量级小的场景，导致多目标优化中棘手的“负迁移跷跷板”问题。因此对于不同场景我们需要相应子网络来进行区分

然而，已有的多任务模型比如ESSM、MMOE、PLE等并不适合多场景任务。一个最大的原因是在做任务模型中，我们显式的有多个目标的label，因此在多个任务中，我们可以最终在各个任务子塔构建每个任务的loss并且通过loss融合来进行学习。但在多场景中，我们优化的只有一个任务，因此多场景下模型的设计核心就在于“如何将各个场景分发到不同子网络”，让不同场景的子网络间相对独立。这也就是STAR模型想要解决的地方

STAR模型结构

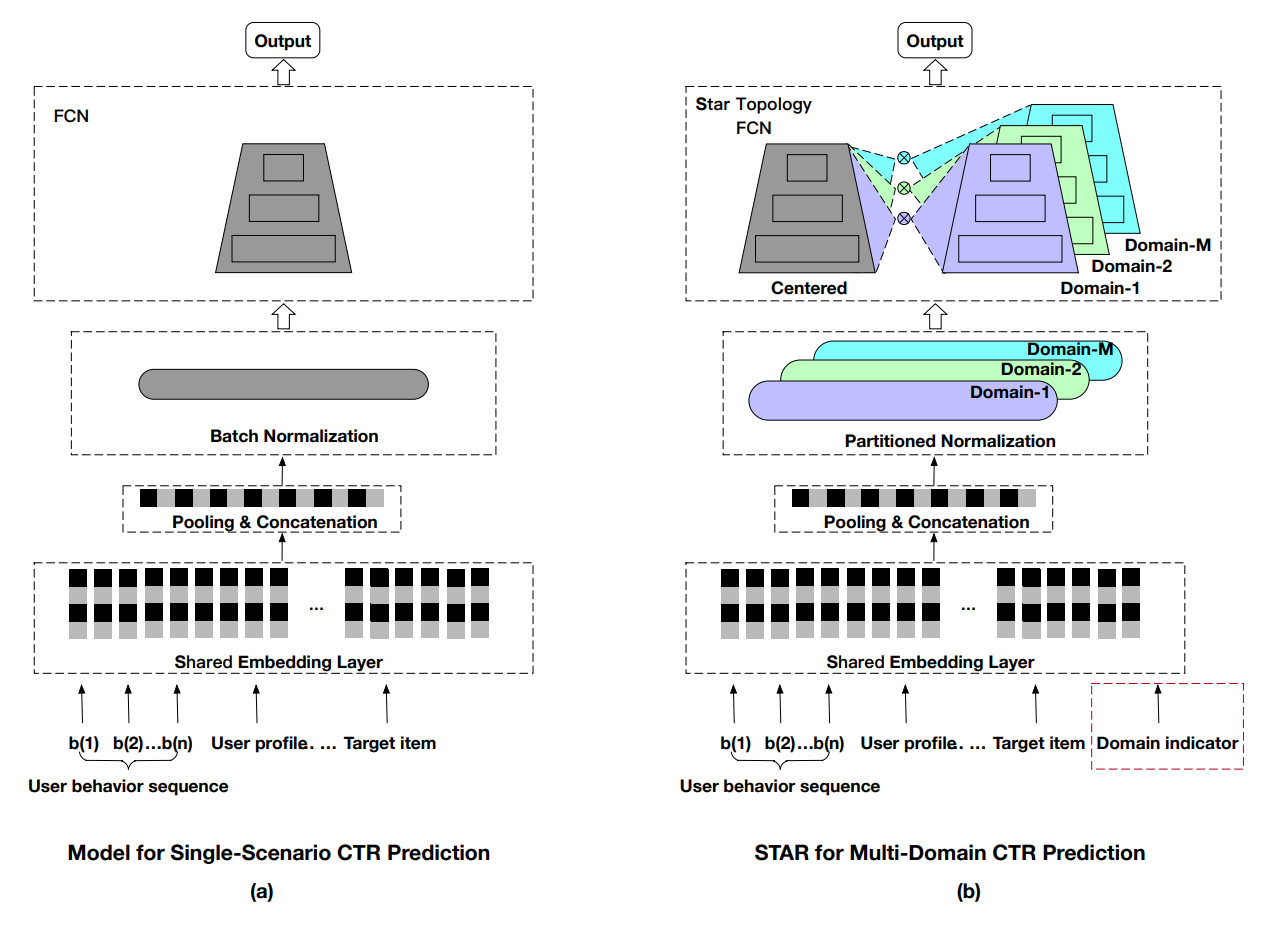
STAR模型结构如上图所示，其中左边为一个典型的embedding+MLP单目标模型，而右边则是STAR模型结构，其中彩色部分既是与单目标模型的区分所在。STAR模型主要创新点在于：

将一个Batch中的Batch Norm改为分不同场景下的Partitioned Norm
共享+领域形式的star型FCN网络结构：STAR topology FCN
用于领域区分的辅助网络

Partitioned Norm

PN层主要是Batch Norm层为了适应多场景任务改进而来。由于多场景下不同场景数据略有区分，而Batch Norm中是所有场景训练数据混合输入的，因此为了满足不同场景需求，将原本的Batch Norm改为分不同场景分别Norm。具体做法也很简单，一个典型的Batch Norm公式如下：

$$z′=\gamma \frac{z - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta$$

其中z为输入，$\mu$和$\sigma$是batch数据的均值和方差，$\epsilon$是为了防止除0的极小数，$\gamma$和$\beta$则是可训练参数

而Partitioned Norm则是很简单地引入场景相关的可训练参数$\gamma_p$和$\beta_p$，并简单地进行相乘/相加耦合，论文并没说实现方式细节，但并不难做到，比如最简单的方式就是把原来的定义参数向量改为embedding lookup获得场景相关参数向量

$$z′=(\gamma \times \gamma_p) \frac{z - \mu}{\sqrt{\sigma^2 + \epsilon}} + \beta + \beta_p$$

在test时，同样相应的$\mu$和$\sigma$也换成对应场景数据的$\mu_p$和$\sigma_p$，当然，为了训练、测试计算方便，在STAR模型训练中一般要求一个batch都是来自于同一个场景，不过这点个人感觉这点无所谓，毕竟真实线上数据来时肯定是随机的，而这样要求说实话对训练速度影响也不大

STAR topology FCN

对于共享+领域形式，前文也提到MMOE、PLE这种独立子网络的方式并不容易做（但也不是不能做，像最近的AESM^2模型就尝试设计了一个贼复杂的门控来切分不同场景子网络），因此STAR想的方法就是像改造Batch Norm一样改造FCN，给原本的$z=f_{act}(W \times x + b)$的W和b也加上场景相关的$W_p$和$b_p$，毕竟我lookup不了一个网络，我还是可以lookup一个网络的某个参数的。因此，STAR改造后的FCN公式如下

$$z=f_{act}(W_p^\star \times x+ b_p^\star)$$

$$W_p^\star = W_p \otimes W$$

$$b_p^\star = b_p + b$$

基本上这种做法也是简单有效的，也基本可以确保在不使用门控的前提下，达到类似共享+领域的推理形式

辅助网络Auxiliary Network

为了可以直接导入场景相关信息，STAR使用的方式是使用将场景特征与其他特征embedding后concat，然后使用一个浅层辅助网络$s_a$来获得结果，并将$s_a$ output和主网络$s_m$ output相加，最终输出logit是：

$$logit=softmax(s_m+s_a)$$

不过个人觉得“和其他concat”这里存疑，因为按照直接思考的话做场景区分也不需要和其他特征concat，场景特征已经足够了。这种处理方法更像一种Wide & Deep，既然想要引入场景的浅层信息了，那不如直接把其他特征的浅层信息拿过来提升效果

模型效果

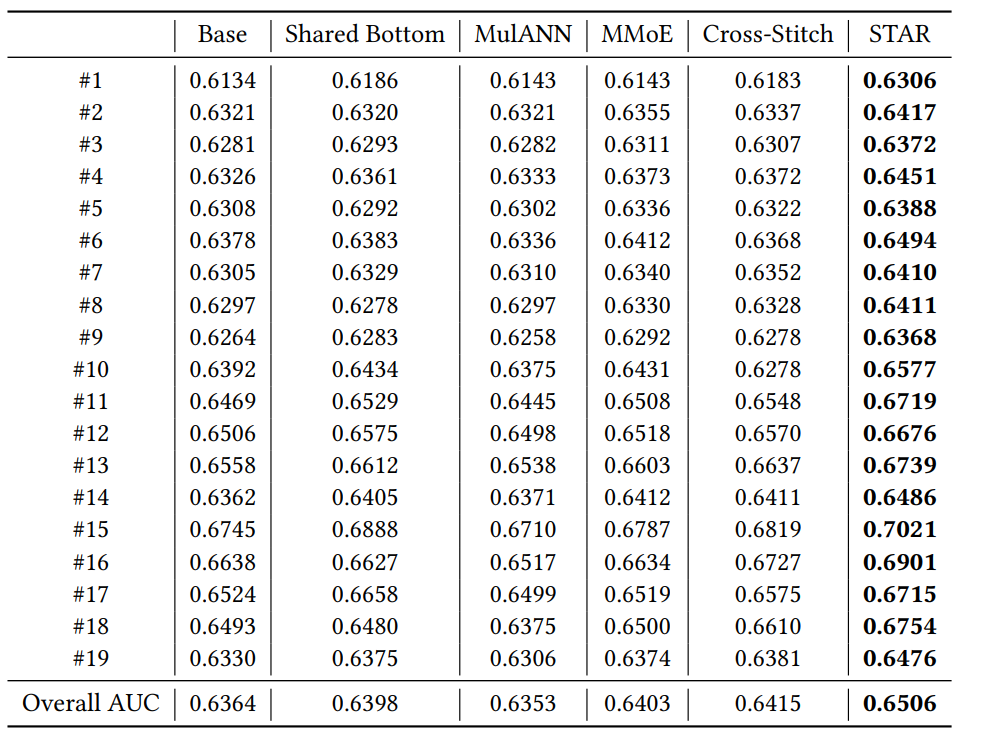
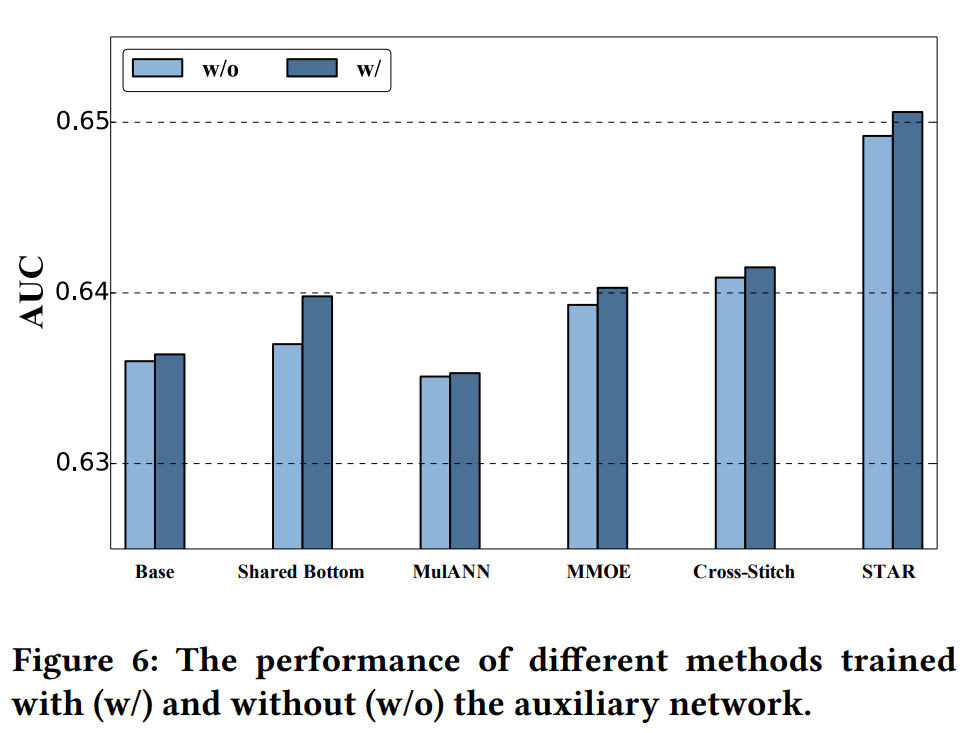
STAR result AUC STAR result Auxiliary

离线结果，整体AUC有约1.4pp的提升。在线结果CTR整体提升8%，RPM整体提升6%

此外，由于模型上线serving后一般会进行在线学习不断更新，由于不同时间段各场景流量比例不同（比如某时间段某场景数据占绝对主导），因此这对模型网络结构损害较大，因此STAR模型在在线学习时还专门工程设计了一个数据缓存区，保证送入学习的各场景的数据比例基本保持稳定。这可以看出此模型工业界实践很深，这些学术研究时很难注意到的trick一般只会在真实实践时才会遇到并尝试解决